Question-89
Let \(( X,Y) \sim \text{Uniform}( D)\), where \(D:=[ 0,2] \times [ 0,2]\). Find \(P( X+Y< 2)\). Enter your answer correct to one decimal place.
\(0.5\)
The joint PDF of \(X,Y\) is:
\[ f_{XY}( x,y) =\begin{cases} \frac{1}{4} , & 0\leqslant x,y\leqslant 2\\ 0, & \text{otherwise} \end{cases} \]
Now, consider the set of points satisfying \(X+Y< 2\). We can visualize this as the shaded region given below:
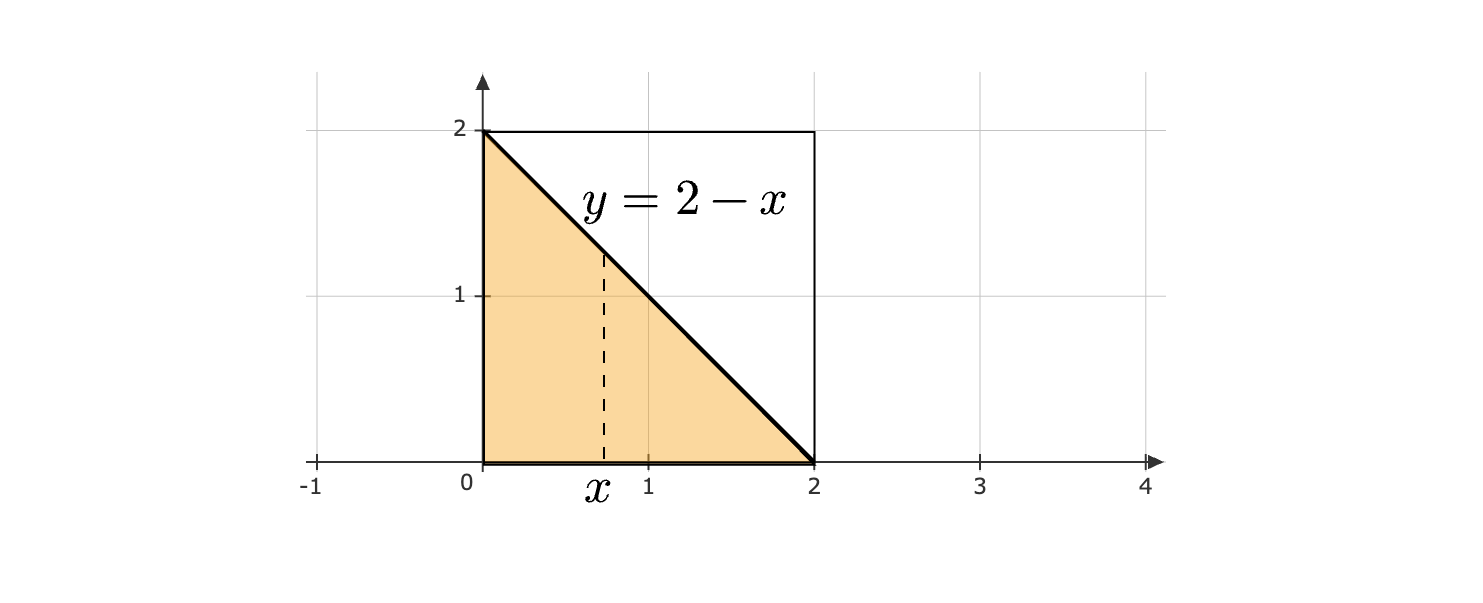
We can now find the required probability by integrating the PDF over the orange region. We will allow \(x\) to range from \(0\) to \(2\). For any \(x\), the value of \(y\) ranges from \(0\) to \(2-x\).
\[ \begin{aligned} P( X+Y< 2) & =\int\limits _{0}^{2}\left[\int\limits _{0}^{2-x}\frac{1}{4} dy\right] dx\\ & \\ & =\int\limits _{0}^{2}\frac{2-x}{4} dx\\ & \\ & =0.5 \end{aligned} \]
