Question-42
Consider the neural network shown in the figure with
inputs: \(u,v\)
weights: \(a,b,c,d,e,f\)
output: \(y\)
\(R\) denotes the ReLU function, \(R( x) =\max( 0,x)\).
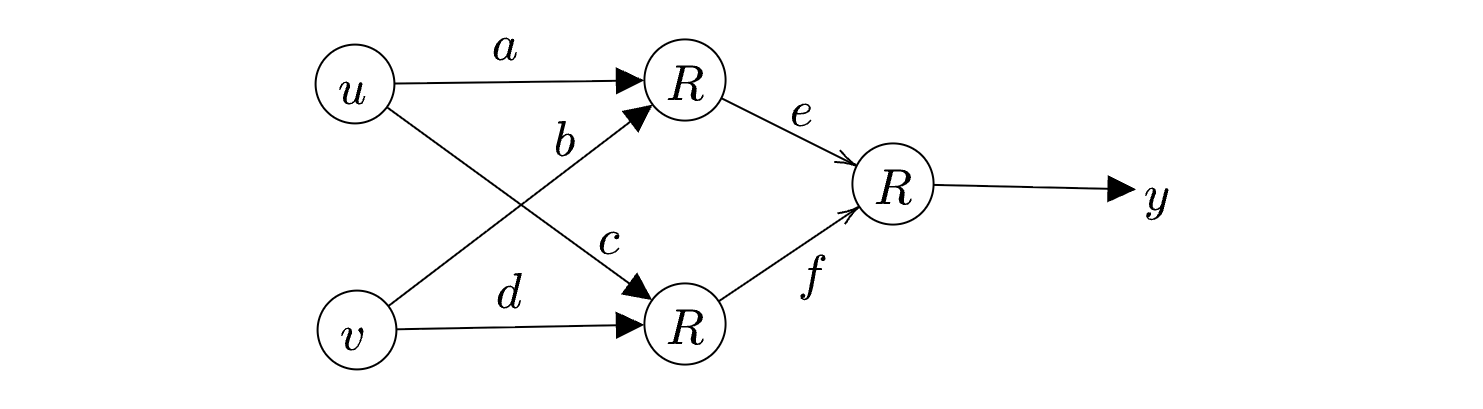
Given \(u=2,v=3\),
\(a=1,b=1,c=1,d=-1,e=4,f=-1\),
which one of the following is correct?
Let us first perform the forward pass:
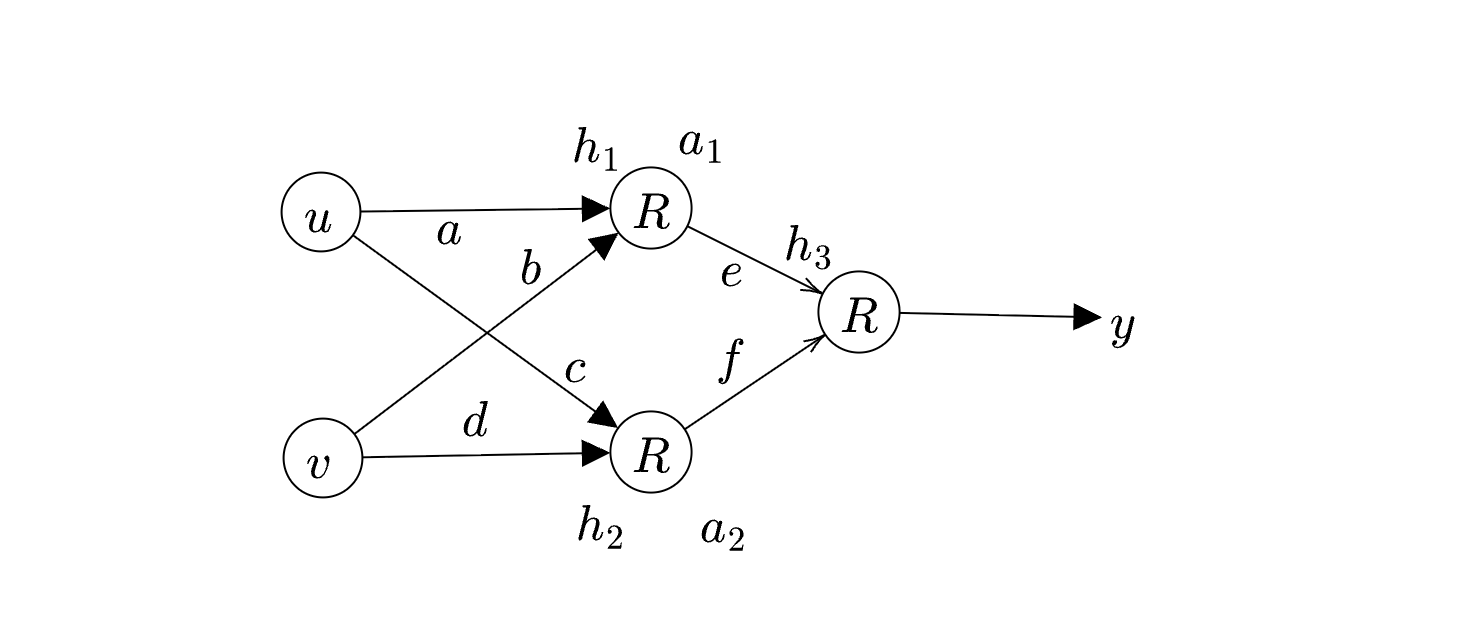
We have:
\[ \begin{array}{ r l l } h_{1} & =au+bv & =5\\ a_{1} & =\max( 0,h_{1}) & =5\\ h_{2} & =cu+dv & =-1\\ a_{2} & =\max( 0,h_{2}) & =0\\ h_{3} & =ea_{1} +fa_{2} & =20\\ y & =\max( 0,h_{3}) & =20 \end{array} \]
The path that is active in influencing \(y\) is shown in green. The other path is not going to be active since \(a_{2} =0\). So we see that \(\cfrac{\partial y}{\partial f} =0\).
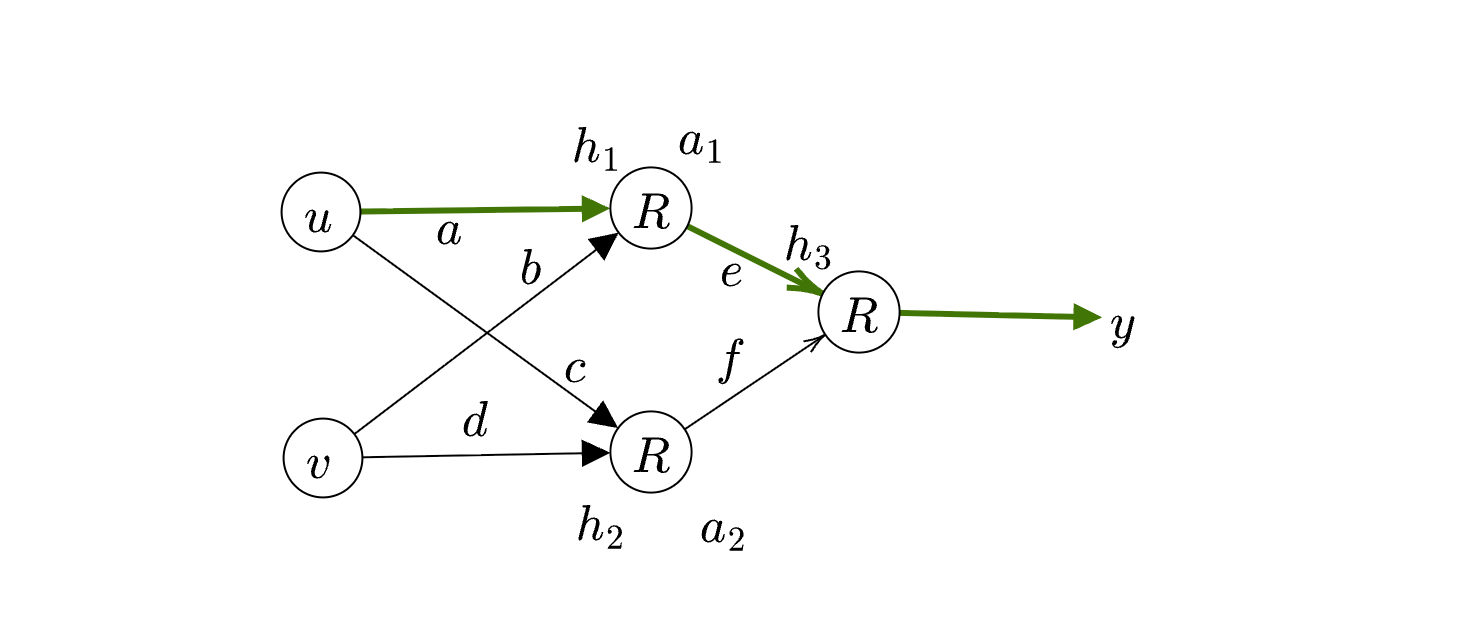
For the green path, we have:
\[ \begin{aligned} \begin{array}{l} \cfrac{\partial y}{\partial a}\\ \end{array} & =\cfrac{\partial y}{\partial h_{3}} \times \cfrac{\partial h_{3}}{\partial a_{1}} \times \cfrac{\partial a_{1}}{\partial h_{1}} \times \cfrac{\partial h_{1}}{\partial a}\\ & \\ & =1\times e\times 1\times u\\ & \\ & =8 \end{aligned} \]
The derivative ReLU is \(1\) whenever the neuron is active.
