Question-55
Consider a two-class problem in \(\mathbb{R}^{d}\) with class labels red and green. Let \(\mu _{\text{red}}\) and \(\mu _{\text{green}}\) be the means of the two classes. Given test sample \(x\in \mathbb{R}^{d}\), a classifier calculates the squared Euclidean distance (denoted by \(||\cdot ||^{2}\)) between \(x\) and the means of the two classes and assigns the class label that the sample \(x\) is closest to. That is, the classifier computes \[ f( x) =||\mu _{\text{red}} -x||^{2} -||\mu _{\text{green}} -x||^{2} \] and assigns the label red to \(x\) if \(f( x) < 0\), and green otherwise. Which of the following is/are correct?
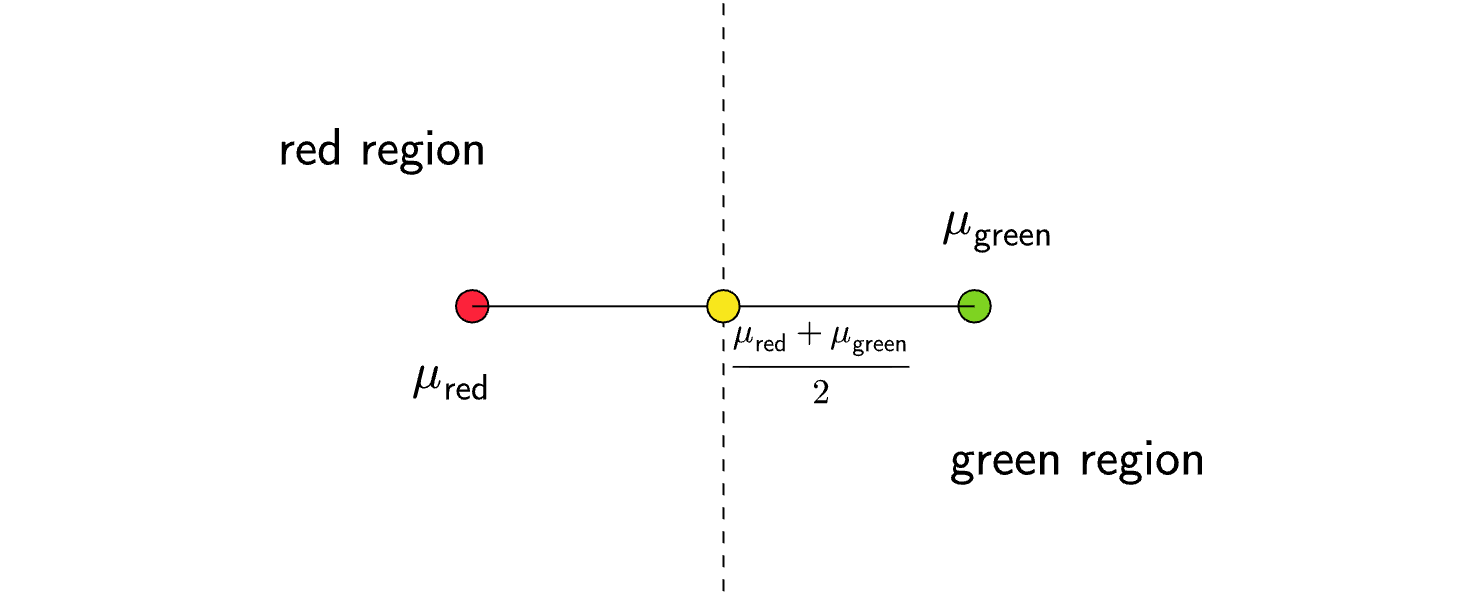
Let us visualize the setup:
We can expand the function \(f\). Using \(r\) for \(\text{red}\) and \(g\) for \(\text{green}\):
\[ \begin{aligned} f( x) & =||\mu _{r} -x||^{2} -||\mu _{g} -x||^{2}\\ & =||\mu _{r} ||^{2} +||x||^{2} -2\cdot \mu _{r}^{T} x\\ & -\left( ||\mu _{g} ||^{2} +||x||^{2} -2\cdot \mu _{g}^{T} x\right)\\ & =\left( ||\mu _{r} ||^{2} -||\mu _{g} ||^{2}\right)\\ & +2\cdot ( \mu _{g} -\mu _{r})^{T} x \end{aligned} \] Setting \(w=2\cdot ( \mu _{g} -\mu _{r})\) and \(b=||\mu _{r} ||^{2} -||\mu _{g} ||^{2}\), we see that \(f( x) =w^{T} x+b\), a linear function of \(x\), where \(w\) and \(b\) are functions of \(\mu _{r}\) and \(\mu _{g}\). As for the sample \(x=0\), we see that \(f( 0) =||\mu _{r} ||^{2} -||\mu _{g} ||^{2}\). This will be assigned green if \(f( 0) \geqslant 0\). Therefore the first option is wrong.
Note: Geometrically, the perpendicular bisector of the line segment joining the two means is the decision boundary of the classifier.
