Question-27

In the diagram, the lines QR and ST are parallel to each other. The shortest distance between these two lines is half the shortest distance between the point P and line QR.

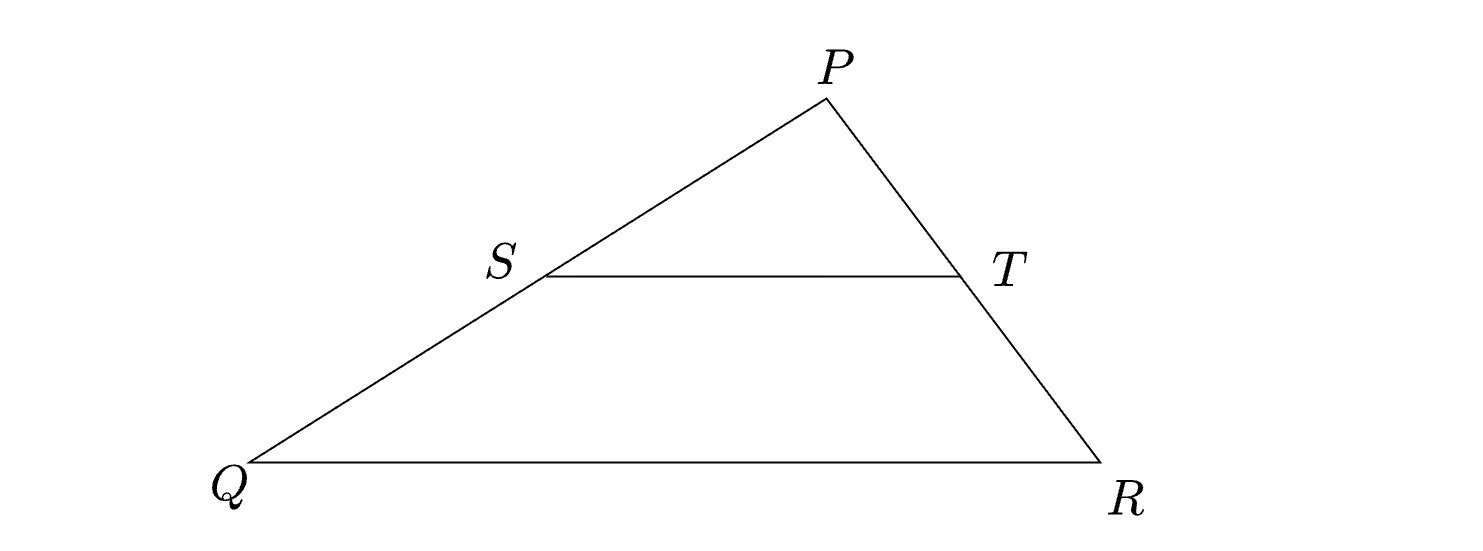
What is the ratio of the area of the triangle PST to the area of the trapezium SQRT?

• 1/3
• 1/4
• 2/5
• 1/2

NoteAnswer

• 1/3
• 1/4
• 2/5
• 1/2

NoteSoluton

Drop a perpendicular from \(P\) to \(QR\). Let it intersect \(ST\) and \(QR\) at \(U\) and \(V\) respectively.

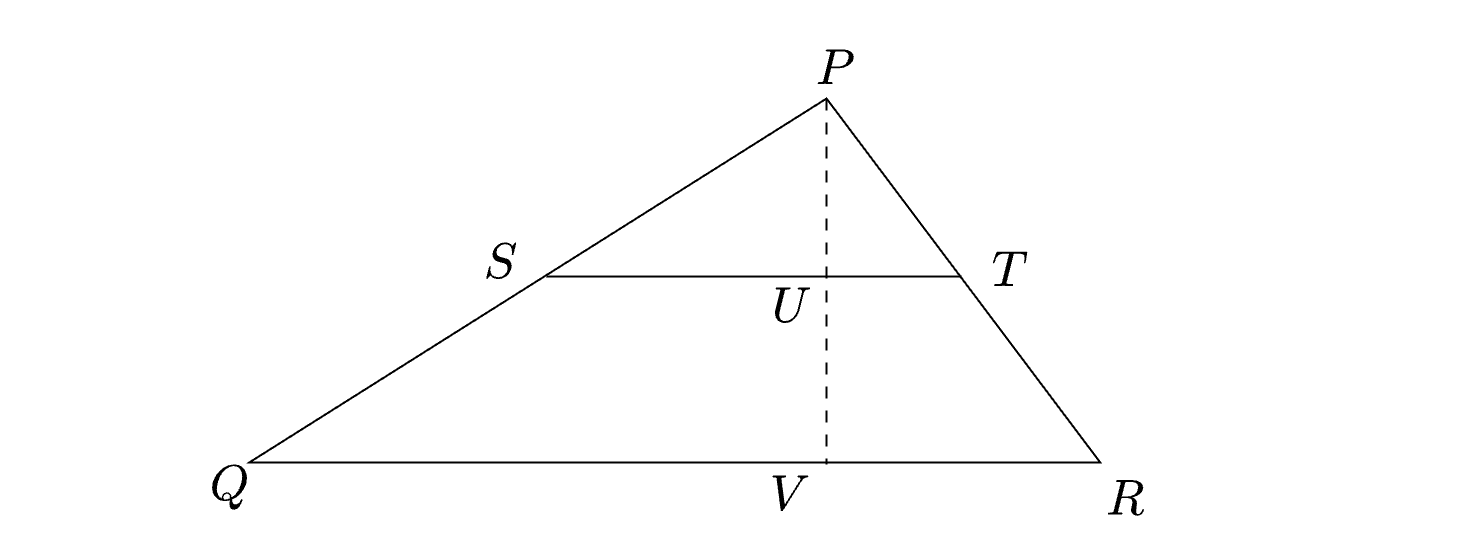
We are given that \(UV = \cfrac{PV}{2}\). This leaves us with \(PU = UV\). Since \(\Delta PST\) and \(\Delta PQR\) are similar, and since \(PU = \cfrac{PV}{2}\), the area of \(\Delta PST\) is one-fourth that of \(\Delta PQR\). The area of the trapezium \(SQRT\) is three-fourth that of \(\Delta PQR\). The required ratio is \(\cfrac{\frac{1}{4}}{\frac{3}{4}} = \cfrac{1}{3}\).